作者:学长
和谐形态的起源
在1935年,金融分析师H.M. Gartley发表了其开创性的著作《股市利润》(”Profits in the Stock Market”),该书在投资界引起了巨大反响。尽管当时正值经济大萧条,Gartley的著作却以每本1500美元的高价限量发行了1000册。这一价格相当于当时可以购买三辆全新福特汽车的价值,反映了其内容的珍贵和影响力。
《股市利润》的第221页和第222页被广泛认为是全书的精髓所在,其中Gartley深入探讨了市场形态分析的复杂性和预测性。他提出的理论不仅在当时具有划时代的意义,而且至今仍被金融市场的分析师和交易者广泛研究和应用。通过这些分析,Gartley为理解市场动态和预测价格走势提供了重要的视角和工具。
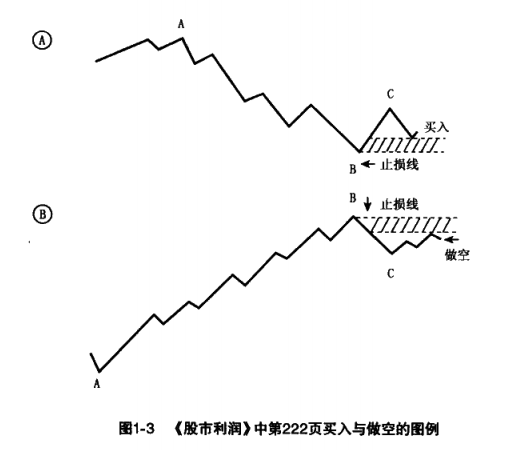
图1-3 展示了H.M. Gartley在《股市利润》中第222页所描述的形态图。我们所讨论的和谐形态正是基于Gartley在该页提出的形态进一步发展而来。尽管Gartley的原始著作并未提供如此精细的形态分析,但其在第221至222页中展示的两张价格模型图,无疑为后续研究者提供了极大的启发。
在金融市场分析领域,交易专家Larry Pesavento对Gartley形态的推广和细化工作功不可没。他在2010年出版的《交易形态精要》一书中,进一步丰富了Gartley形态的应用和理解。此外,1999年Scott Carney的著作《和谐的交易者》也对基于Gartley形态的技术形态进行了深入探讨。Carney在书中介绍了多种以Gartley形态为基础的交易模式,为我们即将学习的技术形态提供了坚实的理论基础。
通过这些专家的不懈努力和深入研究,和谐形态分析已经成为交易者在市场预测和策略制定中不可或缺的工具。这些形态不仅在理论上具有高度的系统性和科学性,而且在实际交易中也显示出了显著的有效性和实用性。
斐波那契数列
在1202年,意大利数学家莱昂纳多·斐波那契在其著作《珠算原理》中,通过一个关于兔子繁殖的有趣问题引入了斐波那契数列的概念。尽管斐波那契并非交易领域的专家,但他的数列在金融交易和市场分析中扮演着极其重要的角色。
斐波那契数列不仅在数学上具有深远的意义,其衍生的比率在技术分析中被广泛引用。交易者经常使用这些比率,如0.382、0.618、0.786等,来识别市场趋势中的潜在回撤水平。这些比率被称为“神奇数字”,在交易策略中具有指导意义。
在和谐形态交易系统中,我们将利用这些斐波那契比率来制定精确的交易计划,以期捕捉市场的波动和趋势。以下是斐波那契兔子问题的详细阐述:
斐波那契兔子问题解析:
设想一个理想化的兔子繁殖模型:每对新生兔子在出生后的第二个月便具备繁殖能力,并在每个月末产生一对新的兔子。假设没有兔子死亡,我们来探究一年内兔子数量的增长情况:
- 第一个月:新生的兔子尚未成熟,因此总数为1对。
- 第二个月:第一对兔子成熟并繁殖出1对新的兔子,总数达到2对。
- 第三个月:第一对成熟的兔子再次繁殖,而第二对尚未成熟,总数增加至3对。

以此类推,每个月兔子的总数遵循斐波那契数列的增长模式,即每个数字都是前两个数字的和。这种增长模式不仅在数学上具有美感,更在交易策略中展现出其独特的价值。通过深入理解斐波那契数列及其比率,交易者可以更精准地把握市场动态,优化交易决策。
斐波那契数列,由以下数字构成:1, 1, 2, 3, 5, 8, …,展现了一个特定的序列模式。该数列的一个显著特征是每一项都是其前两项之和,即满足递推关系:an+2 = an + an+1。此外,连续两个斐波那契数之间的比值趋近于黄金分割比(约为1.618:1或1:0.618)。例如,233/144和987/610等比值。
斐波那契数列还展现出两个有趣的数学性质:
- 数列中任意一项的平方等于其相邻两项的乘积加减1,即an^2 = an-1 * an+1 ± 1。
- 对于数列中任意四个连续的斐波那契数,中间两项的乘积(内积)与最外侧两项的乘积(外积)相差1,即an * an+1 = an-1 * an+2 ± 1。
这些性质不仅揭示了斐波那契数列的数学美感,而且在多个学科领域,包括数学、计算机科学和金融分析中,都有着广泛的应用。
斐波那契分割线
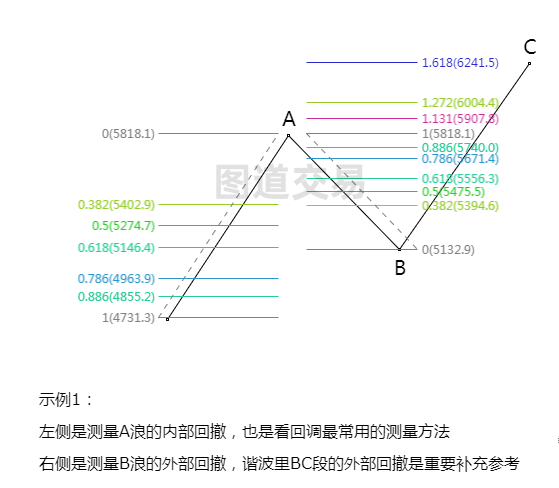
在交易市场中,精通斐波那契数列及其应用对于分析价格行为至关重要。斐波那契数列中最著名的比例是0.618,亦称为黄金分割比。在进行斐波那契分析时,我们通常采用三种主要方法:内部回撤、外部回撤和价格扩展。
汇聚区是斐波那契分析中的一个关键概念,它指的是多个斐波那契比例线在同一价格区域内的交汇点。这些区域往往预示着潜在的支撑或阻力水平,因此对交易者来说具有极高的监控价值。汇聚区可能由多种不同的斐波那契比例线组成,包括内部回撤的不同比例、内部与外部回撤的组合,或者是回撤与扩展的密集区域。然而,如果仅由相同测量方法得出的相同斐波那契比例线构成的区域,则不被视为汇聚区。
在内部回撤分析中,50%和61.8%的比例最为关键,紧接着是38.2%和78.6%。外部回撤分析中常用的比例包括127%、161.8%和262%。斐波那契扩展常用的比例有61.8%、100%和161.8%。通过深入理解并应用斐波那契分析,交易者可以更好地把握市场节奏,识别潜在的交易机会。
斐波那契汇聚区
在使用斐波那契工具进行市场分析之前,理解汇聚区这一概念至关重要。汇聚区指的是在应用多个斐波那契比例时,价格在某一狭窄区间内出现重合的现象。这一现象通常标志着潜在的支撑或阻力水平,对交易决策具有显著影响。
汇聚区可能由以下不同情况组成:
- 多个内部回撤比例的密集区域。
- 内部回撤与价格扩展的交汇区域。
- 外部回撤与内部回撤或扩展的重叠区域。
值得注意的是,仅由相同测量方法得出的同一斐波那契比例所形成的区域,并不构成真正的汇聚区。
在具体的斐波那契分析中,常用的斐波那契比例包括0.5(50%)、0.618(61.8%),其次是0.382(38.2%)、0.786(78.6%)和0.886。在外部回撤中,常用的比例有1.13、1.27、1.414、1.618(161.8%)、2.00和2.618。
斐波那契同向投影
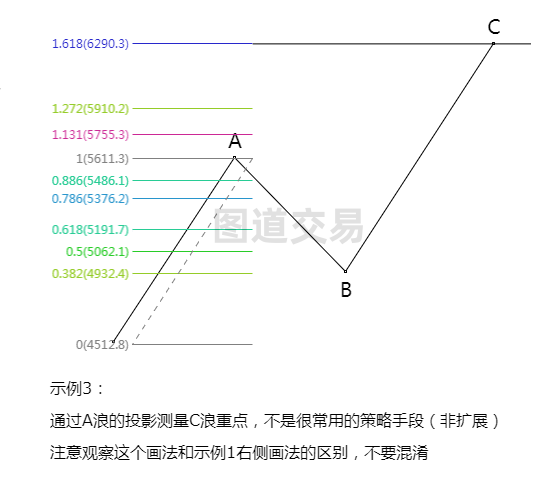
斐波那契扩展
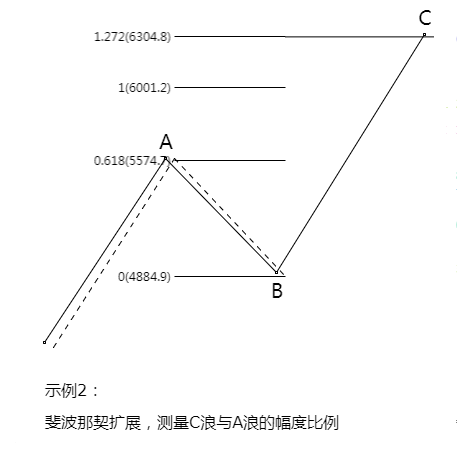
内回撤与外回撤